Build regression model from a set of candidate predictor variables by removing predictors based on p values, in a stepwise manner until there is no variable left to remove any more.
Usage
ols_step_backward_p(model, ...)
# S3 method for default
ols_step_backward_p(
model,
p_val = 0.3,
include = NULL,
exclude = NULL,
hierarchical = FALSE,
progress = FALSE,
details = FALSE,
...
)
# S3 method for ols_step_backward_p
plot(x, model = NA, print_plot = TRUE, details = TRUE, ...)Arguments
- model
An object of class
lm; the model should include all candidate predictor variables.- ...
Other inputs.
- p_val
p value; variables with p more than
p_valwill be removed from the model.- include
Character or numeric vector; variables to be included in selection process.
- exclude
Character or numeric vector; variables to be excluded from selection process.
- hierarchical
Logical; if
TRUE, performs hierarchical selection.- progress
Logical; if
TRUE, will display variable selection progress.- details
Logical; if
TRUE, will print the regression result at each step.- x
An object of class
ols_step_backward_p.- print_plot
logical; if
TRUE, prints the plot else returns a plot object.
Value
ols_step_backward_p returns an object of class "ols_step_backward_p".
An object of class "ols_step_backward_p" is a list containing the
following components:
- model
final model; an object of class
lm- metrics
selection metrics
References
Chatterjee, Samprit and Hadi, Ali. Regression Analysis by Example. 5th ed. N.p.: John Wiley & Sons, 2012. Print.
See also
Other backward selection procedures:
ols_step_backward_adj_r2(),
ols_step_backward_aic(),
ols_step_backward_r2(),
ols_step_backward_sbc(),
ols_step_backward_sbic()
Examples
# stepwise backward regression
model <- lm(y ~ ., data = surgical)
ols_step_backward_p(model)
#>
#>
#> Stepwise Summary
#> -------------------------------------------------------------------------
#> Step Variable AIC SBC SBIC R2 Adj. R2
#> -------------------------------------------------------------------------
#> 0 Full Model 736.390 756.280 586.665 0.78184 0.74305
#> 1 alc_mod 734.407 752.308 584.276 0.78177 0.74856
#> 2 gender 732.494 748.406 581.938 0.78142 0.75351
#> 3 age 730.620 744.543 579.638 0.78091 0.75808
#> -------------------------------------------------------------------------
#>
#> Final Model Output
#> ------------------
#>
#> Model Summary
#> -------------------------------------------------------------------
#> R 0.884 RMSE 184.276
#> R-Squared 0.781 MSE 38202.426
#> Adj. R-Squared 0.758 Coef. Var 27.839
#> Pred R-Squared 0.700 AIC 730.620
#> MAE 137.656 SBC 744.543
#> -------------------------------------------------------------------
#> RMSE: Root Mean Square Error
#> MSE: Mean Square Error
#> MAE: Mean Absolute Error
#> AIC: Akaike Information Criteria
#> SBC: Schwarz Bayesian Criteria
#>
#> ANOVA
#> -----------------------------------------------------------------------
#> Sum of
#> Squares DF Mean Square F Sig.
#> -----------------------------------------------------------------------
#> Regression 6535804.090 5 1307160.818 34.217 0.0000
#> Residual 1833716.447 48 38202.426
#> Total 8369520.537 53
#> -----------------------------------------------------------------------
#>
#> Parameter Estimates
#> ------------------------------------------------------------------------------------------------
#> model Beta Std. Error Std. Beta t Sig lower upper
#> ------------------------------------------------------------------------------------------------
#> (Intercept) -1178.330 208.682 -5.647 0.000 -1597.914 -758.746
#> bcs 59.864 23.060 0.241 2.596 0.012 13.498 106.230
#> pindex 8.924 1.808 0.380 4.935 0.000 5.288 12.559
#> enzyme_test 9.748 1.656 0.521 5.887 0.000 6.419 13.077
#> liver_test 58.064 40.144 0.156 1.446 0.155 -22.652 138.779
#> alc_heavy 317.848 71.634 0.314 4.437 0.000 173.818 461.878
#> ------------------------------------------------------------------------------------------------
#>
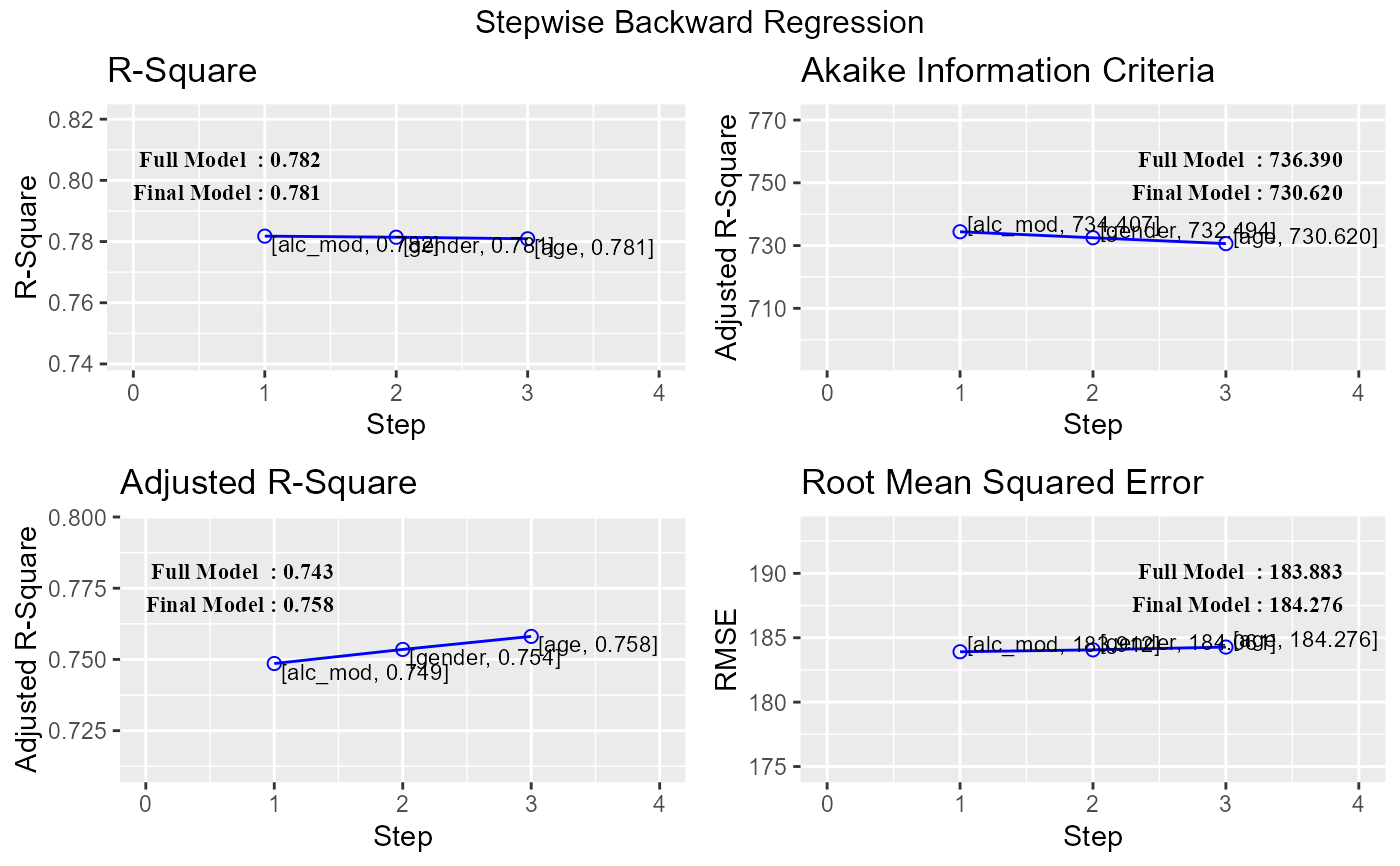
# stepwise backward regression plot
model <- lm(y ~ ., data = surgical)
k <- ols_step_backward_p(model)
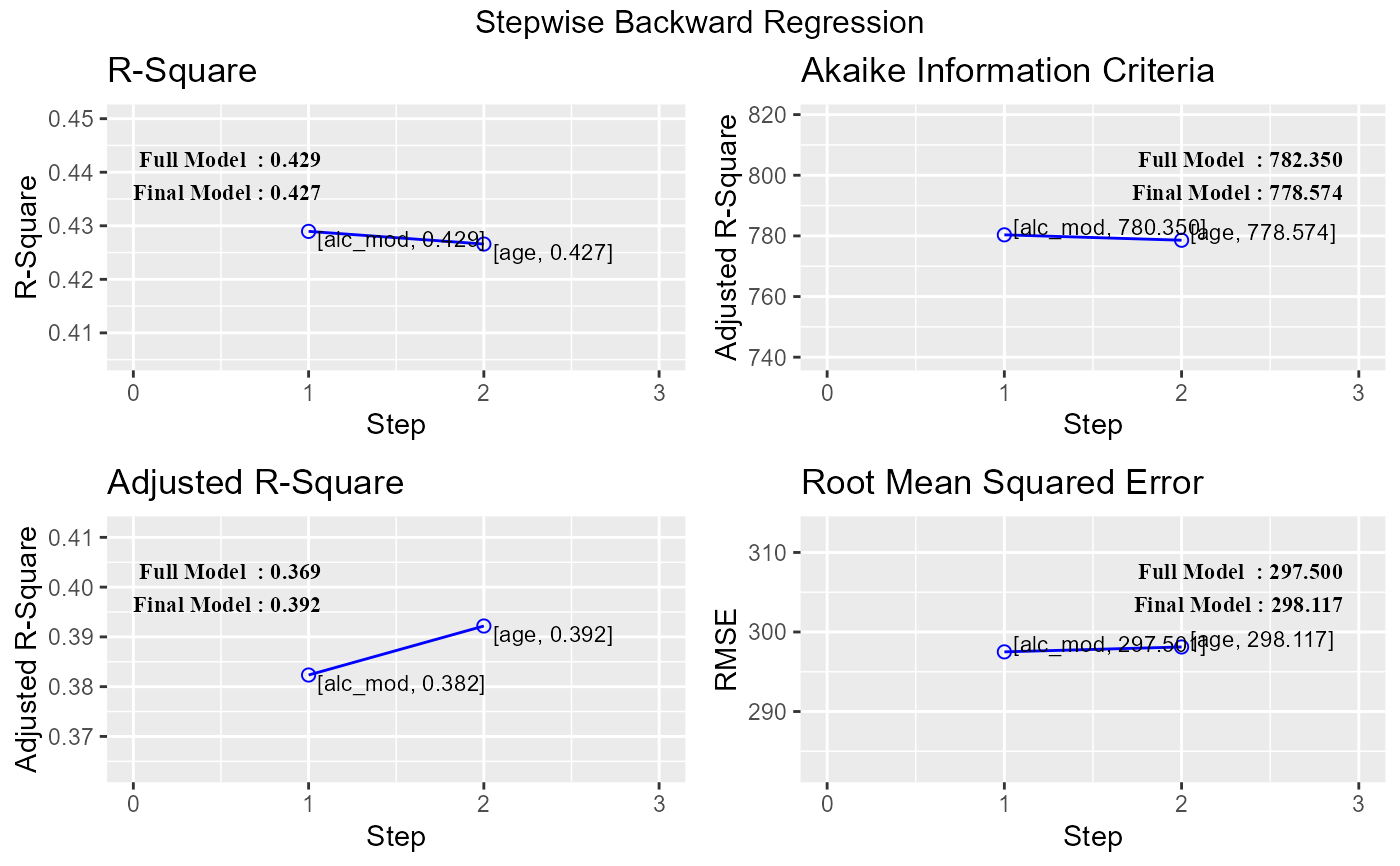
plot(k)
# selection metrics
k$metrics
#> step variable r2 adj_r2 aic sbc sbic mallows_cp
#> 1 1 alc_mod 0.7817703 0.7485615 734.4068 752.3077 584.2757 7.014100
#> 2 2 gender 0.7814169 0.7535127 732.4942 748.4061 581.9383 5.086996
#> 3 3 age 0.7809054 0.7580831 730.6204 744.5433 579.6377 3.192498
#> rmse
#> 1 183.9121
#> 2 184.0610
#> 3 184.2762
# final model
k$model
#>
#> Call:
#> lm(formula = paste(response, "~", paste(c(include, cterms), collapse = " + ")),
#> data = l)
#>
#> Coefficients:
#> (Intercept) bcs pindex enzyme_test liver_test alc_heavy
#> -1178.330 59.864 8.924 9.748 58.064 317.848
#>
# include or exclude variables
# force variable to be included in selection process
ols_step_backward_p(model, include = c("age", "alc_mod"))
#>
#>
#> Stepwise Summary
#> -------------------------------------------------------------------------
#> Step Variable AIC SBC SBIC R2 Adj. R2
#> -------------------------------------------------------------------------
#> 0 Full Model 736.390 756.280 586.665 0.78184 0.74305
#> 1 gender 734.478 752.379 584.323 0.78148 0.74823
#> -------------------------------------------------------------------------
#>
#> Final Model Output
#> ------------------
#>
#> Model Summary
#> -------------------------------------------------------------------
#> R 0.884 RMSE 184.034
#> R-Squared 0.781 MSE 39758.610
#> Adj. R-Squared 0.748 Coef. Var 28.400
#> Pred R-Squared 0.683 AIC 734.478
#> MAE 137.950 SBC 752.379
#> -------------------------------------------------------------------
#> RMSE: Root Mean Square Error
#> MSE: Mean Square Error
#> MAE: Mean Absolute Error
#> AIC: Akaike Information Criteria
#> SBC: Schwarz Bayesian Criteria
#>
#> ANOVA
#> -----------------------------------------------------------------------
#> Sum of
#> Squares DF Mean Square F Sig.
#> -----------------------------------------------------------------------
#> Regression 6540624.486 7 934374.927 23.501 0.0000
#> Residual 1828896.051 46 39758.610
#> Total 8369520.537 53
#> -----------------------------------------------------------------------
#>
#> Parameter Estimates
#> ------------------------------------------------------------------------------------------------
#> model Beta Std. Error Std. Beta t Sig lower upper
#> ------------------------------------------------------------------------------------------------
#> (Intercept) -1145.835 239.628 -4.782 0.000 -1628.181 -663.488
#> age -0.889 2.612 -0.025 -0.340 0.735 -6.146 4.369
#> alc_mod 7.490 64.294 0.009 0.116 0.908 -121.927 136.907
#> bcs 61.533 24.019 0.248 2.562 0.014 13.184 109.882
#> pindex 8.961 1.855 0.381 4.832 0.000 5.228 12.694
#> enzyme_test 9.864 1.722 0.528 5.729 0.000 6.398 13.330
#> liver_test 53.731 42.828 0.145 1.255 0.216 -32.478 139.939
#> alc_heavy 319.282 84.051 0.315 3.799 0.000 150.096 488.467
#> ------------------------------------------------------------------------------------------------
#>
# use index of variable instead of name
ols_step_backward_p(model, include = c(5, 7))
#>
#>
#> Stepwise Summary
#> -------------------------------------------------------------------------
#> Step Variable AIC SBC SBIC R2 Adj. R2
#> -------------------------------------------------------------------------
#> 0 Full Model 736.390 756.280 586.665 0.78184 0.74305
#> 1 gender 734.478 752.379 584.323 0.78148 0.74823
#> -------------------------------------------------------------------------
#>
#> Final Model Output
#> ------------------
#>
#> Model Summary
#> -------------------------------------------------------------------
#> R 0.884 RMSE 184.034
#> R-Squared 0.781 MSE 39758.610
#> Adj. R-Squared 0.748 Coef. Var 28.400
#> Pred R-Squared 0.683 AIC 734.478
#> MAE 137.950 SBC 752.379
#> -------------------------------------------------------------------
#> RMSE: Root Mean Square Error
#> MSE: Mean Square Error
#> MAE: Mean Absolute Error
#> AIC: Akaike Information Criteria
#> SBC: Schwarz Bayesian Criteria
#>
#> ANOVA
#> -----------------------------------------------------------------------
#> Sum of
#> Squares DF Mean Square F Sig.
#> -----------------------------------------------------------------------
#> Regression 6540624.486 7 934374.927 23.501 0.0000
#> Residual 1828896.051 46 39758.610
#> Total 8369520.537 53
#> -----------------------------------------------------------------------
#>
#> Parameter Estimates
#> ------------------------------------------------------------------------------------------------
#> model Beta Std. Error Std. Beta t Sig lower upper
#> ------------------------------------------------------------------------------------------------
#> (Intercept) -1145.835 239.628 -4.782 0.000 -1628.181 -663.488
#> age -0.889 2.612 -0.025 -0.340 0.735 -6.146 4.369
#> alc_mod 7.490 64.294 0.009 0.116 0.908 -121.927 136.907
#> bcs 61.533 24.019 0.248 2.562 0.014 13.184 109.882
#> pindex 8.961 1.855 0.381 4.832 0.000 5.228 12.694
#> enzyme_test 9.864 1.722 0.528 5.729 0.000 6.398 13.330
#> liver_test 53.731 42.828 0.145 1.255 0.216 -32.478 139.939
#> alc_heavy 319.282 84.051 0.315 3.799 0.000 150.096 488.467
#> ------------------------------------------------------------------------------------------------
#>
# force variable to be excluded from selection process
ols_step_backward_p(model, exclude = c("pindex"))
#>
#>
#> Stepwise Summary
#> -------------------------------------------------------------------------
#> Step Variable AIC SBC SBIC R2 Adj. R2
#> -------------------------------------------------------------------------
#> 0 Full Model 736.390 756.280 586.665 0.78184 0.74305
#> 1 age 754.624 770.536 598.424 0.67070 0.62866
#> 2 gender 752.644 766.566 596.850 0.67058 0.63626
#> 3 alc_mod 750.782 762.716 595.377 0.66973 0.64277
#> -------------------------------------------------------------------------
#>
#> Final Model Output
#> ------------------
#>
#> Model Summary
#> -------------------------------------------------------------------
#> R 0.818 RMSE 226.248
#> R-Squared 0.670 MSE 56411.635
#> Adj. R-Squared 0.643 Coef. Var 33.829
#> Pred R-Squared 0.567 AIC 750.782
#> MAE 171.544 SBC 762.716
#> -------------------------------------------------------------------
#> RMSE: Root Mean Square Error
#> MSE: Mean Square Error
#> MAE: Mean Absolute Error
#> AIC: Akaike Information Criteria
#> SBC: Schwarz Bayesian Criteria
#>
#> ANOVA
#> -----------------------------------------------------------------------
#> Sum of
#> Squares DF Mean Square F Sig.
#> -----------------------------------------------------------------------
#> Regression 5605350.444 4 1401337.611 24.841 0.0000
#> Residual 2764170.093 49 56411.635
#> Total 8369520.537 53
#> -----------------------------------------------------------------------
#>
#> Parameter Estimates
#> ----------------------------------------------------------------------------------------------
#> model Beta Std. Error Std. Beta t Sig lower upper
#> ----------------------------------------------------------------------------------------------
#> (Intercept) -534.711 197.967 -2.701 0.009 -932.540 -136.882
#> bcs 34.471 27.316 0.139 1.262 0.213 -20.422 89.365
#> enzyme_test 7.431 1.929 0.397 3.851 0.000 3.554 11.309
#> liver_test 149.496 43.277 0.403 3.454 0.001 62.528 236.464
#> alc_heavy 292.382 86.822 0.288 3.368 0.001 117.907 466.858
#> ----------------------------------------------------------------------------------------------
#>
# use index of variable instead of name
ols_step_backward_p(model, exclude = c(2))
#>
#>
#> Stepwise Summary
#> -------------------------------------------------------------------------
#> Step Variable AIC SBC SBIC R2 Adj. R2
#> -------------------------------------------------------------------------
#> 0 Full Model 736.390 756.280 586.665 0.78184 0.74305
#> 1 age 754.624 770.536 598.424 0.67070 0.62866
#> 2 gender 752.644 766.566 596.850 0.67058 0.63626
#> 3 alc_mod 750.782 762.716 595.377 0.66973 0.64277
#> -------------------------------------------------------------------------
#>
#> Final Model Output
#> ------------------
#>
#> Model Summary
#> -------------------------------------------------------------------
#> R 0.818 RMSE 226.248
#> R-Squared 0.670 MSE 56411.635
#> Adj. R-Squared 0.643 Coef. Var 33.829
#> Pred R-Squared 0.567 AIC 750.782
#> MAE 171.544 SBC 762.716
#> -------------------------------------------------------------------
#> RMSE: Root Mean Square Error
#> MSE: Mean Square Error
#> MAE: Mean Absolute Error
#> AIC: Akaike Information Criteria
#> SBC: Schwarz Bayesian Criteria
#>
#> ANOVA
#> -----------------------------------------------------------------------
#> Sum of
#> Squares DF Mean Square F Sig.
#> -----------------------------------------------------------------------
#> Regression 5605350.444 4 1401337.611 24.841 0.0000
#> Residual 2764170.093 49 56411.635
#> Total 8369520.537 53
#> -----------------------------------------------------------------------
#>
#> Parameter Estimates
#> ----------------------------------------------------------------------------------------------
#> model Beta Std. Error Std. Beta t Sig lower upper
#> ----------------------------------------------------------------------------------------------
#> (Intercept) -534.711 197.967 -2.701 0.009 -932.540 -136.882
#> bcs 34.471 27.316 0.139 1.262 0.213 -20.422 89.365
#> enzyme_test 7.431 1.929 0.397 3.851 0.000 3.554 11.309
#> liver_test 149.496 43.277 0.403 3.454 0.001 62.528 236.464
#> alc_heavy 292.382 86.822 0.288 3.368 0.001 117.907 466.858
#> ----------------------------------------------------------------------------------------------
#>
# hierarchical selection
model <- lm(y ~ bcs + alc_heavy + pindex + age + alc_mod, data = surgical)
ols_step_backward_p(model, 0.1, hierarchical = TRUE)
#>
#>
#> Stepwise Summary
#> -------------------------------------------------------------------------
#> Step Variable AIC SBC SBIC R2 Adj. R2
#> -------------------------------------------------------------------------
#> 0 Full Model 782.350 796.273 630.574 0.42896 0.36948
#> 1 alc_mod 780.350 792.284 628.324 0.42896 0.38234
#> 2 age 778.574 788.519 626.262 0.42659 0.39218
#> -------------------------------------------------------------------------
#>
#> Final Model Output
#> ------------------
#>
#> Model Summary
#> -------------------------------------------------------------------
#> R 0.653 RMSE 298.117
#> R-Squared 0.427 MSE 95983.505
#> Adj. R-Squared 0.392 Coef. Var 44.127
#> Pred R-Squared 0.269 AIC 778.574
#> MAE 215.068 SBC 788.519
#> -------------------------------------------------------------------
#> RMSE: Root Mean Square Error
#> MSE: Mean Square Error
#> MAE: Mean Absolute Error
#> AIC: Akaike Information Criteria
#> SBC: Schwarz Bayesian Criteria
#>
#> ANOVA
#> -----------------------------------------------------------------------
#> Sum of
#> Squares DF Mean Square F Sig.
#> -----------------------------------------------------------------------
#> Regression 3570345.284 3 1190115.095 12.399 0.0000
#> Residual 4799175.253 50 95983.505
#> Total 8369520.537 53
#> -----------------------------------------------------------------------
#>
#> Parameter Estimates
#> ---------------------------------------------------------------------------------------------
#> model Beta Std. Error Std. Beta t Sig lower upper
#> ---------------------------------------------------------------------------------------------
#> (Intercept) -330.996 216.010 -1.532 0.132 -764.866 102.874
#> bcs 53.710 27.413 0.217 1.959 0.056 -1.351 108.771
#> alc_heavy 410.115 112.012 0.405 3.661 0.001 185.131 635.098
#> pindex 10.223 2.543 0.435 4.021 0.000 5.116 15.330
#> ---------------------------------------------------------------------------------------------
#>
# plot
k <- ols_step_backward_p(model, 0.1, hierarchical = TRUE)
plot(k)
